最小割树
基本定义
$G=(V,E)$表示一个无向图,$c(e)$表示该无向图的边权
一个割是将点集$V$划分为两个集合$S$和$T$的划分
任何一条边$(u,v)\in E$。若$u\in S,v\in T$,那就说这条边为割边
一个割的容量就是所有割边的边权和
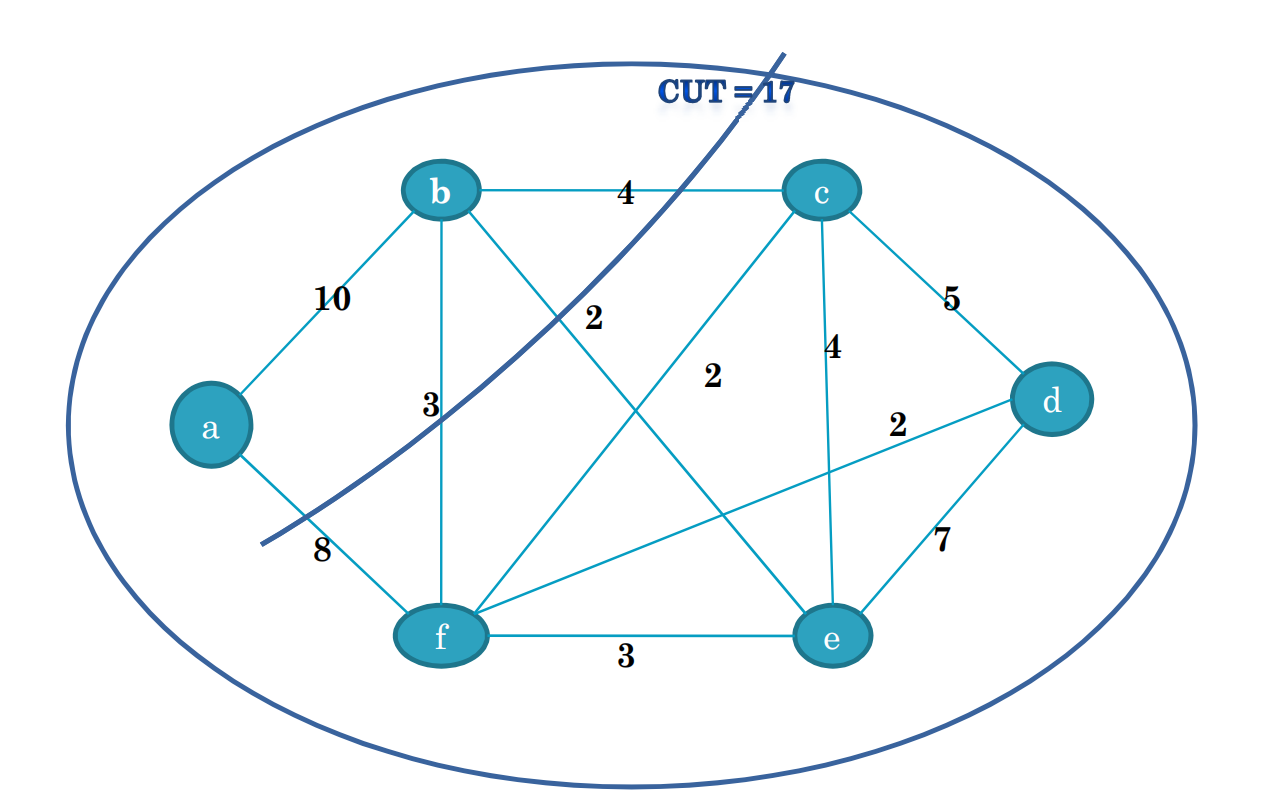
$u-v \space cut$ 是一个$u\in S, v\in T$ 的割
最小$u-v \space cut$是指边权和最小的$u-v \space cut$,这个边权和用$C_{u,v}$表示
$T=(V,F)$为$G=(V,E)$的最小割树需满足:
- 树上任意一条边$(u,v)$的边权为图$G$中$u,v$两点的最小割。断开这条边后分成的两个连通块恰好对应原图最小割的$(S,T)$两个点集
最小割树的构造
- 初始时$T=(V,F)$,$V$为所有的点集,$F=\emptyset$
- 任选两点$u,v$,在$G$中得到两点的最小割$C_{u,v}$,将边$(u,v,C_{u,v})$加入$F$集合中
- 得到上述割的$S,T$集合
- 对$S,T$集合重复执行第二步操作,知道集合大小为1
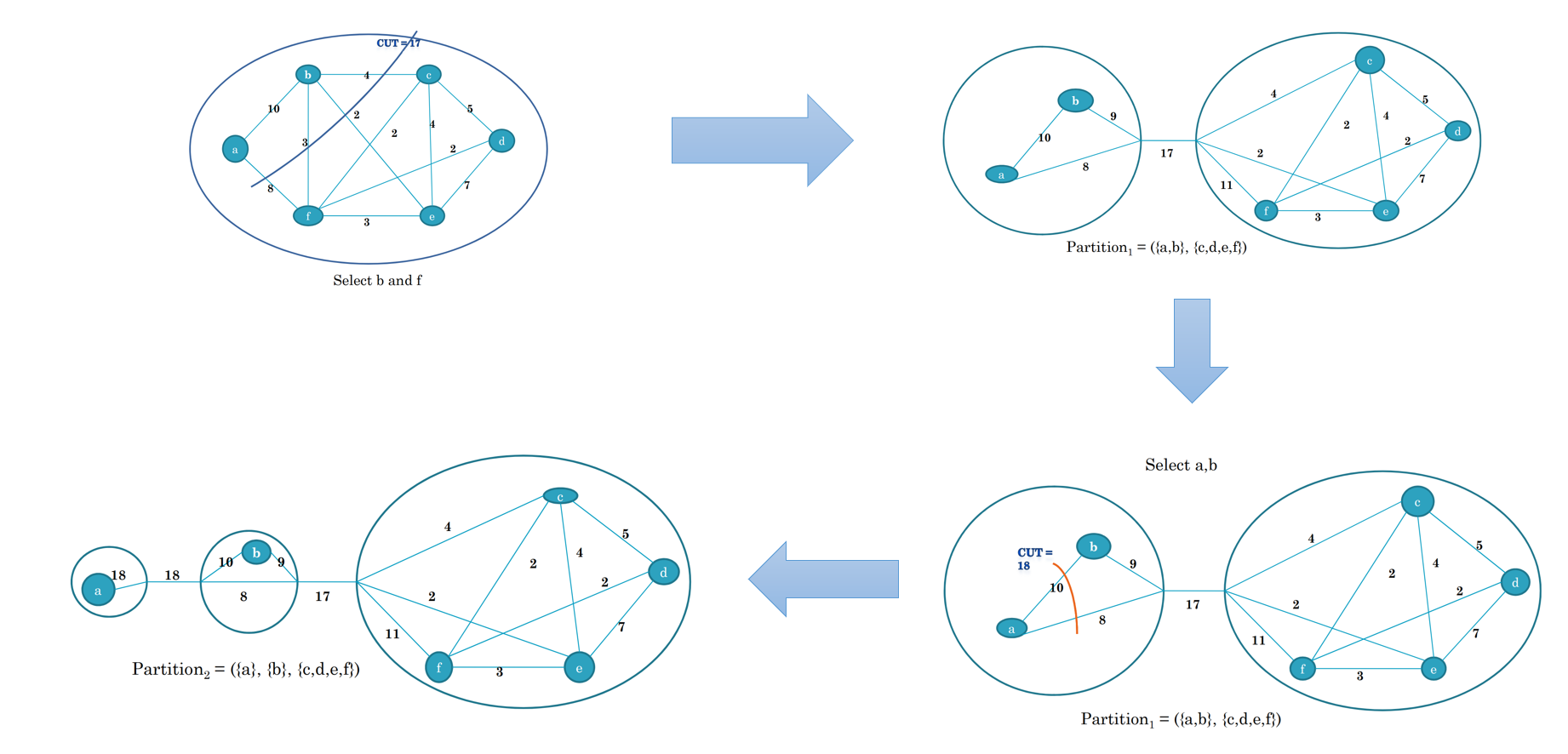
这种构造的做法能否得到最小割树的正确性证明:
设在选择第一对点$(s,t)$的时候得到的最小割为$(S,T)$
第二次在$S$点集中任意选的两点为$(u,v)$得到的最小割为$(U,V)$
现在目标要证:$T \subseteq U \space or \space T \subseteq V$
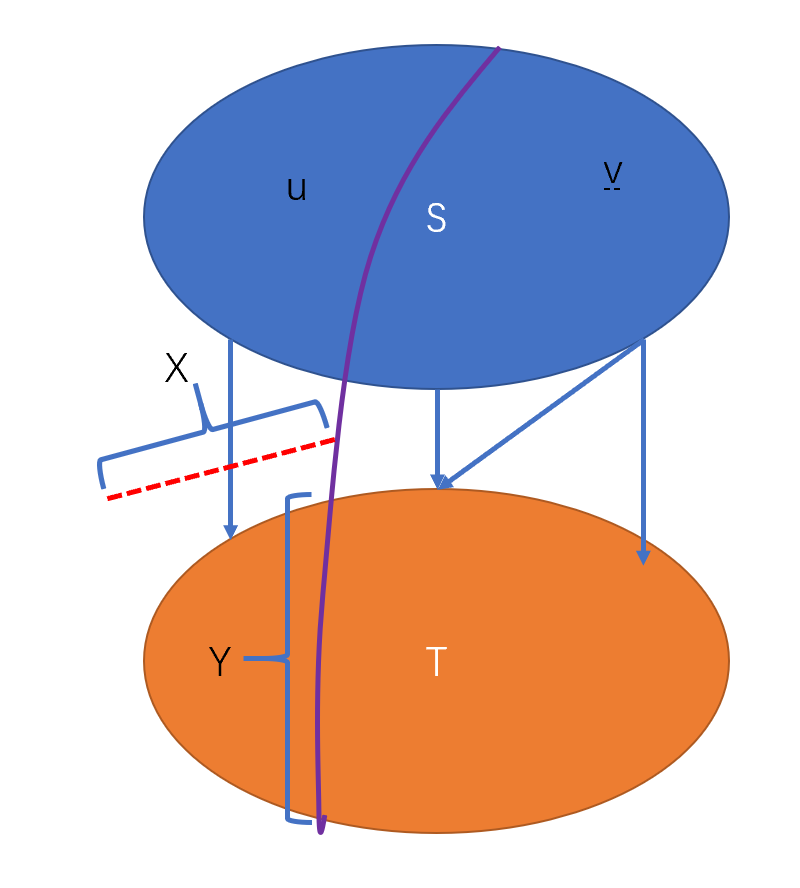
显然X部分割的边的容量不大于Y部分割的边的容量,否则与$(S,T)$是$(s,t)$的最小割矛盾
证毕。
任意两点的最小割等于最小割树上两点路径上的最小边权
引理:对于任意一个无向图的三个点$u,v,w$有,$C_{u,v} \ge \min\{C_{u,w},C_{w,v}\}$
证:若$(U,V)$为$(u,v)$的最小割,设$w\in U$($w\in V$同理)必有 $C_{u,v} \ge C_{w,v}$
推广:对于点集$a_1,\cdots,a_n$有$C_{a_1,a_n} \ge \min\{C_{a_1,a_2},\cdots,C_{a_{n-1},a_n} \}$
由上述引理可知,原图任意两点的最小割一定大于等于最小割树上最两点路径上的最小边权
引理:设$(u,v)$的最小割$(U,V)$,任意点对$(x,y)$,若$x\in U,y\in V$有$C_{x,y} \le C_{u,v}$
由上述引理可知,原图任意两点的最小割一定小于等于最小割树上最两点路径上的最小边权
综上:原图任意两点的最小割一定大于等于最小割树上最两点路径上的最小边权