莫队算法（1）

莫队算法

莫队算法主要用于解决离线的区间问题。一般来说时间复杂度为$O(n\sqrt n)$，对于带修改的莫队算法时间复杂度一般为$O(n^{5/3})$。

普通莫队

考虑这样一个问题：

对于数列 ${a_n}$ 有 $n$ 次询问，每次询问区间 $[l,r]$ 中不同的数的个数。

$n \le 100000$ , $1\le l \le r \le 100000$

一个很显然的想法是，对于每一个询问我们从左到右遍历一遍 $a$ 数组，用另一个数组维护每个数字是否出现，这样就能得到每次询问的答案。

const int n = 100001;
int a[n],cnt[n];
int ask(int l,int r){
    int ret=0;
    for(int i=l;i<=r;i++) cnt[a[i]]=0; //初始化cnt数组
    for(int i=l;i<=r;i++){
        if(cnt[a[i]]==0) ret++; //第一次出现
        cnt[a[i]]++;
    }
    return ret;
}

但是我们这样的算法肯定无法在规定的时间内计算出所有的答案。

分析上述算法，我们发现我们是把每次查询都孤立开来看的。

事实上，假如对于两次相同的询问，我们完全可以利用上一次得到的答案，而省掉一次调用ask函数的时间开销。还有一个显然的问题就是，$n$ 次查询中可能没有两个询问的区间是一模一样的。

即便如此，上面的思考仍然会带给我们一些启发。退而求其次，如果两个询问比较接近，那么我们依然可以借用上一次的询问得到的信息来加速这次询问的查询效率。

例如：$[l_i,r_i]$ 为本次查询的区间，那么下一次询问的区间 $[l_{i+1},r_{i+1}]$ 如何利用 $[l_i,r_i]$ 的信息来加速呢？假如 $l_{i+1} \le l_i \le r_i \le r_{i+1} $ ，对于 $[l_{i+1},r_{i+1}]$ 的查询的ask函数就可以完全保留cnt数组，然后循环遍历 $l_{i+1}->l_i$ 和 $r_i->r_{i+1}$ 。

对于其他诸如 $l_i \le l_{i+1}$ 的时候，同样可以借助 $[l_i,r_i]$ 的信息，只是cnt的数组的初始化部分更新一下。

于是我们就可以写出一个优化的ask函数如下：

int ask(int lastL,int lastR,int l,int r,int lastAns){
    //cnt数组共用
    int ret=lastAns;
    if(l<lastL){ //左边上次未计算的区间贡献答案
        for(int i=l;i<lastL;i++){
            if(cnt[a[i]]==0) ret++; 
            cnt[a[i]]++;
        }
    }
    else if(l>lastL){ //如果左边计算得多了，得将多余区间贡献的答案减掉，并还原cnt数组
        for(int i=lastL;i<l;i++){
            if(cnt[a[i]]==1) ret--;
            cnt[a[i]]--; //
        }
    }
    if(r>lastR){ //右边同理
        for(int i=lastR+1;i<=r;i++){
            if(cnt[a[i]]==0) ret++;
            cnt[a[i]]++;
        }
    }
    else if(r<lastR){
        for(int i=r+1;i<=lastR;i++){
            if(cnt[a[i]]==1) ret--;
            cnt[a[i]]--;
        }
    }
    return ret;
}

到此，我们就基本掌握了莫队算法的核心了，但是还有一个非常重要的问题还没有解决，那就是就算每次我们都在上次询问答案的基础上进行进一步的加工，那么我们的时间复杂度究竟改进了多少？

时间复杂度分析

根据上述算法，很容易知道总的操作次数

从 $\sum_{i=1}^n (r_i-l_i+1)$ 变为了 $(r_1-l_1+1)+\sum_{i=2}^n \vert l_i-l_{i-1} \vert + \vert r_i-r_{i-1} \vert$

很遗憾的是，我们这种优化并没有从本质上改变时间复杂度，即时间复杂度还是 $O(n^2)$ 的。例如给出的查询数据如下：

1 100000
50000 50000
1 100000
50000 50000
......

但是，如果我们通过合理的调整查询的顺序，是否可以改善时间复杂度呢？

答案是肯定的。

对于每一查询 $[l_i,r_i]$ 我们把它看作是二维平面中坐标为 $(l_i,r_i)$ 的点，那么 $\vert l_i-l_{i-1} \vert + \vert r_i-r_{i-1} \vert$ 即为两点之间的曼哈顿距离。$n$个查询区间看作$n$个二维平面的点的话，那么我们的查询顺序不就是连接这$n$个点的那$n-1$条边吗？

那我们的查询顺序不就可以抽象成在这 $n$个点，$\frac{n*(n-1)}{2}$ 边，边权为两点之间的曼哈顿距离，组成的完全图中找出一条路径，使得$n$个点都在此路径上，且这条路径的边权和最小，或者尽量小。

其实也不用是路径。只要是能把这$n$个点完全覆盖就行。

也就是说，要寻找的其实就是曼哈顿最小生成树。

已知曼哈顿最小生成树的边权和是不超过$n\sqrt{n}$ 的

曼哈顿最小生成树也可在$O(n\log{n})$求出。

其实并不需要求出最小曼哈顿生成树

如何简单且高效的找出这条路径呢？这又是莫队算法另一个精妙之处。

莫队算法给出了一种构造方案，可以使得这条路径的边权和在$O(n\sqrt{n})$级别。

构造方案：

• 确定一个常数 $block$ 。（通常情况下 $block=\sqrt{n}$ ）
• 对所有区间进行排序，排序的比较规则如下：
  • 如果 $\frac{l_i}{block}=\frac{l_j}{block}$
    • 按照右端点 $r$ 升序排序
  • 否则
    • 按照左端点升序排序

事实上，这种构造方案相当于将所有的区间分成了 $\frac{n}{block}$ 个块

我们还是将每个区间看作二维平面的点，那么这个示意图如下：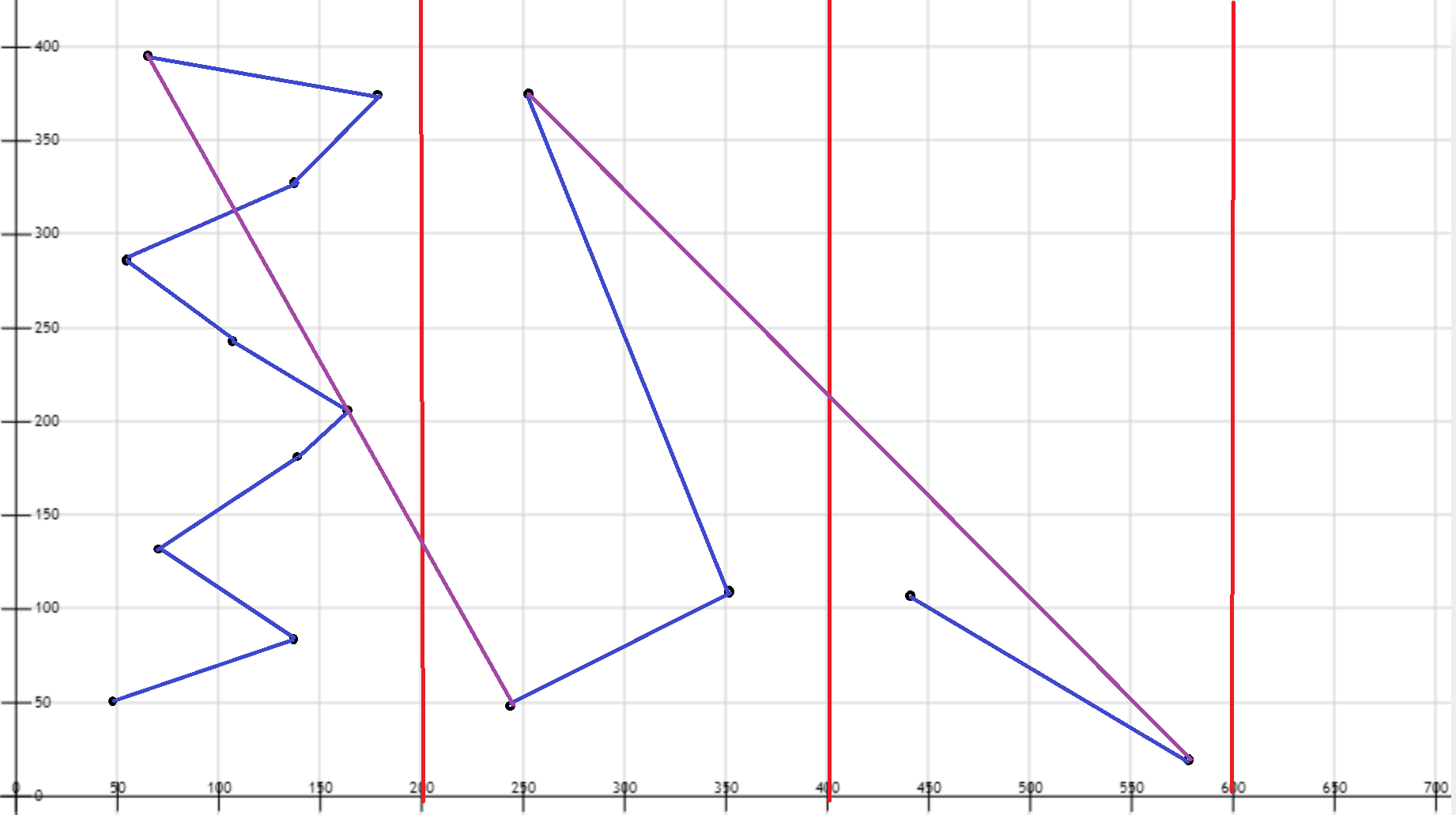

蓝色线中的点表示同一个块中的点之间的转移排序顺序，而紫色的线表示不同块之间的转移顺序。

容易证明，紫色的线只有$\frac{n}{block}=\sqrt n$条（我们先默认$block=\sqrt n$ ），而每条紫线的x坐标之差不超过$\sqrt n$，y坐标之差不超过$n$。故紫线所用的所有开销为$O(n\sqrt n)$。

蓝色的线最多有$n-1$条。每条蓝色的线的x坐标之差不超过$block = \sqrt n$ 。而在单个块中累积的y坐标之差之和不超过$n$。故蓝线所有的开销为$O(n\sqrt n)$。

一开始对区间进行排序的时间复杂度为$O(n\log n)$

综上，莫队总的时间复杂度为$O(n\log n+n\sqrt n)$

莫队算法的应用