分块算法1
分块
分块是一种易用性高、实现简单、单次操作时间复杂度为$O(\sqrt n)$的数据结构。
分块算法几乎可以解决所有线段树和平衡树能解决的问题。
问题引入
对数列$\{a_n\}$有$n$次操作,分别为:
1、修改位置$pos$的值为给定的$val$(单点修改)
2、询问区间$[l,r]$的和(区间查询)
$1 \le n \le 10^5$
这是一道经典的数据结构入门题。
简单分析按照题意的朴素算法的时间复杂度,对于单点修改操作每次为$O(1)$,对于区间查询每次操作的时间复杂度为$O(n)$。故最坏情况下时间复杂度为$O(n^2)$。显然这不能解决题目要求的数据范围。
根据上面的分析可以看到,时间复杂度的瓶颈是在查询过程。想要优化上面的算法,自然就要把重心放在优化查询的时间复杂度。
对于处理区间和问题,一个比较好的做法就是利用前缀做差,即数列的前缀和为$p_i$,那么区间$[l,r]$的和为$p_r-p_{l-1}$。而且通过$O(n)$的预处理所有前缀和后,单次的区间查询的时间复杂度就变成了$O(1)$了。这的确是一个非常巧妙的想法,而且也极大的提高了区间查询的时间复杂度。
但是预处理前缀和后,单点修改操作变得更加复杂了。每次单点修改后,为了维持前缀和信息,需要将单点修该的$pos$位置后面的所有前缀和信息进行更新,使得单点修改的时间复杂度为$O(n)$。这依然无法解决上面的问题。
分块
从上面的分析我们得到了两种修改-查询时间复杂度分别为$O(1)-O(n)$和$O(n)-O(1)$的算法。分块要做的事情正是在上面两种算法中寻找一个平衡点。
如何寻找这个平衡点呢?
假如我们把数列$\{a_n\}$前后均等的分成两个部分(两块),在这两个部分中分别(互不干扰的)应用前缀和的算法,可以发现对于单点修改操作就变为了$O(\frac{n}{2})$,而区间查询的时间复杂度变为$O(2)$(当查询区间横跨两块的时候)。
同样的假如我们把数列$\{a_n\}$前后均等的分成$m$个块呢?对每个块都单独使用前缀和的算法,可以发现对于单点修改操作就变为了$O(\frac{n}{m})$,而区间查询的时间复杂度变为$O(m)$
现在问题我们就得到了很多个修改-查询时间复杂度为$O(\frac{n}{m})-O(m)$的算法。事实上我们发现其实一开始就直接得到的$O(1)-O(n)$的朴素算法就是一种分块的特殊情况(当$m=n$时)
如何确定$m$的值使得$\max\{\frac{n}{m},m\}$最小呢?最小为多少呢?这个$\max\{\frac{n}{m},m\}$就是算法的瓶颈。
当$m=\sqrt n$的时候得到$\max\{\frac{n}{m},m\}=\sqrt n$。即通过调节$m$的取值,可以用上述算法在$O(n\sqrt n)$内解决上面的问题。
容易证明,当 $a*b=n$ 且 $a,b \ge 0$时,$\max\{a,b\}$的最小值为$\sqrt n$。
至此,我们就已经用分块算法在$O(n\sqrt n)$内解决了上面的问题。
分块再分析
事实上上面我们得到的是 $O(\sqrt n)-O(\sqrt n)$算法。
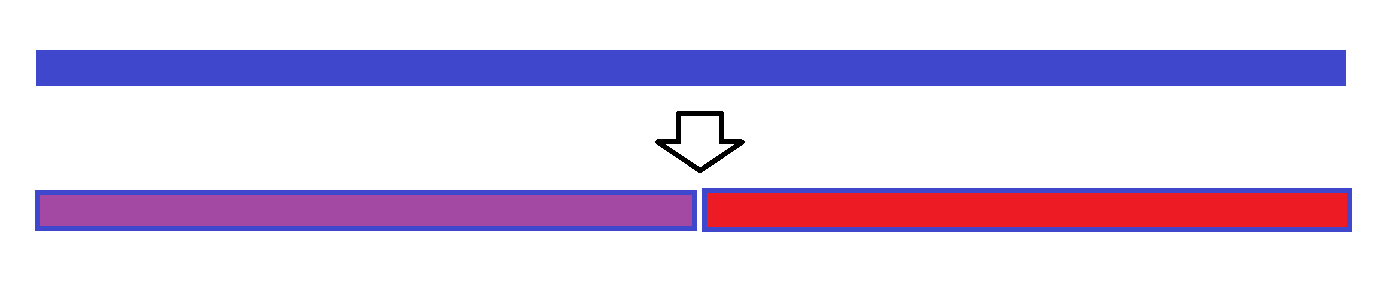
分析上面的算法发现,每次查询的时候,对于$[l,r]$之间的那些整块(蓝色块)都是只需要查询块内元素的总和,只有边角信息(红色块)才需要做朴素算法那样的$p_j-p_i$进行查询。

假如我们在每个块中再维护一个额外的信息——块内值的和,而不在维护块内的前缀和,会发送什么样的变化呢?
这种分块的方法对于修改操作来说时间复杂度将为了$O(1)$,而查询操作的时间复杂度为$O(\sqrt n)$(对于边角信息使用朴素算法扫描,也最多只会有$\sqrt n$个零散点),故修改-查询时间复杂度变为了$O(1)-O(\sqrt n)$。注这种算法的查询操作的常数比上面的查询操作要大。
通过上面的尝试,我们不禁会想,是否存在一种修改-查询时间复杂度$O(\sqrt n)-O(1)$的算法呢?答案是肯定的。我们只需要在修改-查询时间复杂度为$O(1)-O(\sqrt n)$的算法基础上记录一下块内和的前缀信息,再记录块内的前缀信息,就能使修改-查询时间复杂度$O(\sqrt n)-O(1)$。
其实想要得到修改-查询时间复杂度$O(\sqrt n)-O(1)$的做法也可以不使用辅助空间,直接让第$i$块内的最后一个元素记录前$i$个块的前缀和即可。
在很多情况下,我们除了要应对分块带来的时间开销,还需要去计算其他信息,这时候我们就可以根据实际情况选择修改-查询时间复杂度为$O(1)-O(\sqrt n)$的算法或者修改-查询时间复杂度$O(\sqrt n)-O(1)$的算法。
不均等分块
除了上述的均等分的分块算法,当然还有不均等分的分块算法。
例如树状数组可以看着一个按照二进制位进行分块的算法,这样使得单点修改和前缀和查询的时间复杂度变为了$O(\log n)-O(\log n)$。
除此之外,还有按照十进制进行分块的算法:
使得修改-查询时间复杂度为$O(\log_{10}n)-O(\log_{10}{9*n})$
或者修改-查询时间复杂度为$O(\log_{10}{9*n})-O(\log_{10}n)$。